SUDUT-SUDUT BERELASI
Sudut-Sudut Berelasi
Nama: Rizkiah
Kelas: X MIPA 1
Sudut-Sudut Berelasi
Sudut Berelasi – Adalah perluasan definisi dasar ilmu trigonometri tentang kesebangunan pada segitiga siku-siku yang memenuhi untuk sudut kuadran I atau sudut lancip (0 − 90°).
Rumus Sudut Berelasi
Dengan memakai sudut-sudut relasi, kita mampu menghitung nilai perbandingan pada trigonometri untuk sudut pada kuadran lainnya, bahkan untuk sudut yang lebih dari 360°, termasuk juga sudut negatif.
Sudut-sudut yang berelasi atau berhubungan ditunjukkan dengan adanya hubungan antara sudut α dengan sudut (90° ± α), (180° ± α), (270° ± α), (360° ± α), atau -α.
Jika sudut α berelasi dengan sudut (90° - α) atau (π2 - α), maka kedua sudut dinamakan saling berpenyiku. Selanjutnya, jika sudut α berelasi dengan sudut (180° - α) atau (π - α), maka kedua sudut tersebut dinamakan saling berpelurus.
Perbandingan Trigonometri di kuadran.
Oleh karena pada gambar di atas, titik M(x1, y1) adalah bayangan dari titik K(x, y) oleh pencerminkan terhadap garis y = x, makaDengan demikian, relasi antara sudut α dengan sudut (90° - α) atau (π2−α) adalah sebagai berikut:
Contoh:
sin75°=sin(90°−15°)=cos15°
cosπ6=cos(π2−π3)=sinπ3
tan25°=tan(90°−65°
》Perbandingan Trigonometri di Kuadran II
A. Sudut α berelasi dengan sudut (180° - α) atau (π - α)
Contoh:sin120° = sin(180°−60°)=sin60°=123√
cos56π = cos(π−π6)=−cosπ6=−123√
tan135°= tan(180°−45
B. Sudut α berelasi dengan (90° + α) atau (π2 + α)
Misalkan A(x , y), OA = r, dan ∠AOC = α.
Jika α diputar dengan pusat perputaran adalah O(0,0) sejauh 90° dengan arah berlawanan arah putar jarum jam, maka bayangan titik A oleh perputaran tersebut adalah A'(-y , x).
Dengan demikian, ∠AOA' = (90° + α) dan OA = OA' = r.
tan 135° = tan(90° + 45°) = - cot 45° = -1
》Perbandingan Trigonometri di Kuadran III
A. Sudut α berelasi dengan (180° + α) atau (π α)
Mari kita perhatikan gambar berikut:
Relasi antara sudut α dengan sudut (180° + α) adalah sebagai berikutB. Sudut berelasi dengan sudut (270° - α) atau (32π - α)
Misalkan A(x , y), OA = r, dan ∠AOC = α.
Jika titik A dicerminkan terhadap garis y = x, kemudian diputar dengan pusat perputaran adalah O sejauh 180° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A"(-y, -x), dimana ∠AOA' = (270° - α) dan OA = OA" = r
Tentukan nilai dari cos 210° dengan menggunakan relasi (180° + α) dan (270° - α).
》Perbandingan Trigonometri di Kuadran IV
A. Sudut α berelasi dengan (360° - α) atau (2π - α)
Dengan demikian, relasi antara sudut α dengan sudut (360° - α) atau (2π - α) adalah sebagai berikut:
Contoh:
B. Sudut α berelasi dengan sudut (270° + α) atau (32π + α)
Jika titik A(x , y) dengan OA = r dan ∠AOB = α diputar dengan pusat O(0,0) sejauh 270° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A'(y , x), dimana∠AOA' = (270° + α) dan OA = OA' = r.
Berdasarkan gambar di atas, relasi antara sudut α dan sudut (270° + α) adalah sebagai berikut:C. Sudut α berelasi dengan sudut (-α)
Mari kita perhatikan gambar berikut.
∠QOP = α → berlawanan arah dengan arah putar jarum jam
∠QOP' = -α → searah dengan arah putar jarum jam
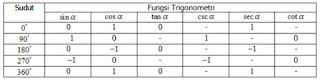
Nilai perbandingan trigonometri pada batas kuadran dapat kita tentukan dengan menggunakan lingkaran satuan.
Jika sudut A lebih besar dari 360°, maka sudut A harus diubah terlebih dahulu sehingga berbentuk (θ + k.360°) dengan k = 1, 2, 3, 4, ....
Berikut adalah contoh soal yang menggunakan sudut berelasi.
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya !
sin 50°
tan 40°
cos 35°
Jawab :
sin 50° = sin (90° − 400°)
= cos 40°
tan 40° = tan (90° − 50°)
= cot 50°
cos 35° = cos (90° − 55°)
= sin 55°
Ketiganya bernilai positif, karena sudut 50°, 40° dan 35° berada di kuadran I.
2. Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
tan 153°
sin 243°
cos 333°
Jawab :
Sudut 153° adapada kuadran II, hingga tan 153° memiliki nilai negatif.
tan 153° = tan (180° − 27°)
= -tan 27°
Sudut 243° ada pada kuadran III, sehingga sinus memiliki nilai negatif.
sin 243° = sin (270° − 27°)
= -cos 27°
Sudut 333° ada pada kuadran IV, hingga cosinus memiliki nilai positif.
cos 333° = cos (360° − 27°)
= cos 27°













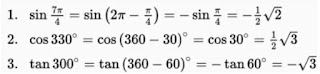







Komentar
Posting Komentar